Imbasan Icosahedron untuk pelekatan: templat A4, A3 dengan elaun, dimensi. Skim

Angka yang dibuat daripada kertas boleh berbeza.. Walau bagaimanapun, selalunya keutamaan diberikan kepada bentuk geometri. Salah satunya ialah icosahedron (corak untuk melekat), yang boleh dipanggil kompleks dan mudah pada masa yang sama. Kompleks kerana ia mempunyai banyak muka - 20 keping, dan ia mempunyai lebih banyak tepi - 30 keping. Mudah kerana ia simetri sepenuhnya mengenai pusatnya.

Penerangan tentang angka tersebut

Icosahedron (corak untuk gluing diberikan di bawah dalam artikel) adalah angka yang mendapat namanya kira-kira 100 tahun yang lalu. Ia berasal dari angka Yunani kuno "ikosi", yang diterjemahkan sebagai "20". Bahagian lain nama itu berasal dari perkataan "hedra", yang bermaksud "tepi". Ternyata nama itu boleh diterjemahkan dari bahasa Yunani sebagai "20 sisi".

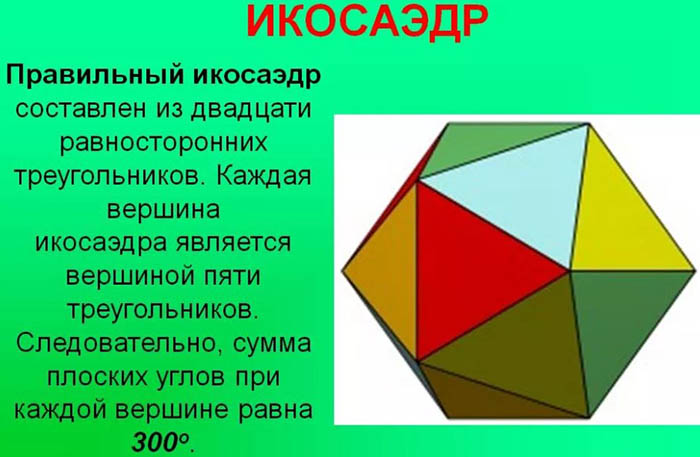
Untuk membolehkan badan geometri tiga dimensi dipanggil ikosahedron biasa, ia mesti memenuhi syarat berikut:

• ia mesti mempunyai tepat 20 muka (tidak lebih dan tidak kurang);
• setiap muka ini mestilah segi tiga sekata. Dalam geometri, segitiga dipanggil sekata jika semua sudutnya adalah sama. Setiap sudut segi tiga ini mempunyai nilai 60 darjah.

Ikosahedron ialah polihedron biasa dan merupakan salah satu daripada lima pepejal yang dipanggil "Platonic".

Ciri-cirinya yang lain adalah seperti berikut:

• bilangan sisi setiap 20 muka ialah 3;
• bilangan bucu (titik sambungan sisi muka) – 12;
• bilangan tepi (tepi muka) yang menumpu pada setiap bucu (titik) ialah 5;
• jumlah bilangan rusuk - 30;
• bilangan paksi simetri - 15;
• bilangan satah simetri – 15.

Walau bagaimanapun, semua ciri ini mengikuti dari dua ciri utama yang disebutkan di atas. Jika rajah mempunyai 20 muka dan jika setiap muka adalah segi tiga sekata, maka ia sudah menjadi ikosahedron sekata sebenar dengan semua sifatnya.

Icosahedron (corak untuk gluing tidak sukar walaupun untuk pemula) adalah angka yang kawasannya mudah ditentukan, walaupun terdapat banyak muka. Di samping itu, ia boleh diwakili sebagai kawasan sapuan. Jika luas 1 daripada 20 segi tiga yang merupakan muka rajah itu diketahui, maka sudah cukup untuk mendarabkan nombor ini dengan 20.

Sebagai contoh, jika luas setiap segi tiga ialah 4 cm persegi, maka jumlah luas semua permukaan icosahedron akan sama dengan 80 meter persegi. Untuk melakukan ini, 4 mesti didarab dengan 20.

Jenis utama

Icosahedron yang boleh dibuat daripada kertas boleh berbeza.

Contohnya, jika:

• Jika anda menggunakan hanya satu warna kertas dalam kerja anda, angka itu akan menjadi satu warna;
• ia akan menjadi kertas berwarna, anda boleh membuat icosahedron pelbagai warna, yang akan bermain dengan warna yang berbeza dan kelihatan lebih cantik.

Selalunya icosahedron dibuat, yang kelihatan seperti bola sepak dalam warna, dengan segitiga putih berselang-seli dengan yang hitam. Pada hakikatnya ia tidak akan menjadi bola, kerana ia jauh dari bulat. Lebih sukar untuk dilaksanakan ialah icosahedron, yang mempunyai bentuk bintang. Sudah ada aspek di sini yang menonjol dengan latar belakang orang lain.

Yang paling cantik ialah icosahedron, dihiasi dengan pelbagai elemen hiasan. Ini boleh menjadi sebarang hiasan: sesuatu yang berkilat, terang - sesuatu yang boleh dilekatkan dengan mudah pada permukaan kertas. Icosahedron ini boleh digunakan sebagai mainan Tahun Baru dan digantung pada pokok Krismas.

Terdapat banyak icosahedra dalam geometri. Sebahagian daripada mereka mempunyai lebih simetri, manakala yang lain, sebaliknya, kurang simetri. Yang paling biasa ialah icosahedron biasa - yang mempunyai tepat 20 muka yang serupa. Dalam matematik, ikosahedron biasa boleh dipanggil sama ada badan cembung atau tidak cembung.

Walau apa pun, setiap daripada mereka mempunyai 20 muka dan 1.5 kali lebih tepi. Kedua-duanya mempunyai apa yang dipanggil simetri ixosahedral. Walau bagaimanapun, selalunya bentuk cembung yang dipanggil ikosahedron biasa, manakala bentuk tidak cembung termasuk dalam kategori ikosahedra yang hebat.

Icosahedron (imbasan untuk pelekatan) boleh diwakili oleh pilihan berikut:

Rajah	Penerangan
Ikosahedron cembung	Ia mempunyai 20 muka dan 12 bucu. Pepejal geometri ini mempunyai dwi polyhedron. Ia dipanggil dodecahedron biasa. Ia mempunyai 3 muka 5 sisi biasa di sekeliling setiap bucu.
Icosahedron yang hebat	Ia mempunyai tepat 20 muka, setiap satunya adalah segi tiga sekata. Walau bagaimanapun, puncaknya bukan 5-gon, tetapi pentagram. Atas sebab inilah tepi bersilang secara geometri. Apabila mereka bersilang, tiada tepi baru terbentuk. Dwi polyhedron bagi icosahedron yang hebat ialah dodecahedron yang hebat. Ia mempunyai 3 muka tertumpu di sekeliling setiap bucu, setiap satunya ialah 5-gon.
Icosahedra berbintang	Jika muka atau tepi polihedron mengembang, maka apabila mereka menyentuh, bentuk bintang terbentuk. Ini berlaku secara simetri, jadi badan yang terhasil mempunyai simetri yang sama seperti angka asal. Kerja saintifik Coxeter "59 icosahedra" menyenaraikan hampir 60 jenis stellated polyhedra ini. Ramai daripada mereka mempunyai aspek yang berasingan dalam setiap 20 pesawat. Banyak badan lain mempunyai lebih daripada 1 muka di dalam pesawat. Mereka boleh dibentuk dengan menggabungkan polyhedra yang lebih ringkas.
Pseudoicosahedron	Ikosahedron biasa yang dipintal, menyebabkan simetrinya berkurangan.
Ikosahedron Jessen	Jika jasad geometri tiga dimensi mempunyai 12 muka, setiap satunya ialah segi tiga sama kaki, dan muka ini disusun sedemikian rupa sehingga membentuk badan tidak cembung, maka angka ini sudah pun dipanggil Jessen icosahedron (atau ortogonal icosahedron). Ia mempunyai sudut 2 sisi tepat. Salah satu cirinya ialah ia boleh terurai sama dengan heksagon, setiap mukanya adalah segi empat sama. Ini bermakna ia boleh dibahagikan kepada polyhedra kecil, dan kemudian digunakan untuk membentuk heksagon dengan muka yang sama saiz. Heksagon sedemikian ialah kubus.

Bagaimana untuk membuat icosahedron biasa daripada kertas?

Pembangunan untuk melekatkan Icosahedron untuk pembuatan memerlukan penyediaan bahan dan alat berikut:

• kertas. Ia boleh beralun, putih, atau berwarna. Ketumpatannya juga boleh berbeza-beza;
• gunting. Diperlukan untuk memotong angka dengan saiz dan bentuk yang diperlukan;
• gam. Pilihan terbaik ialah PVA biasa, kerana ia mengambil masa yang lama untuk kering, yang cukup untuk menghapuskan kemungkinan ralat;
• pembaris. Tanpa itu, ia akan menjadi sangat sukar untuk membengkokkan kertas secara sama rata di sepanjang garis lipatan.

Anda juga boleh menggunakan bahan tambahan untuk menghias kraf kertas anda. Ini soal citarasa dan imaginasi.

Selepas menyediakan semua bahan dan alat, anda boleh meneruskan terus ke proses kreatif.

Kerja berlaku dalam peringkat berikut:

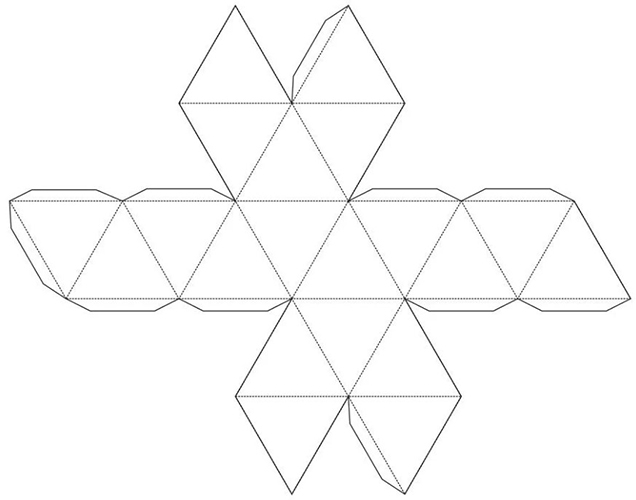
1. Cetak templat yang telah siap pada pencetak dan pindahkan ke bahan yang disediakan. Penjagaan mesti diambil semasa pemindahan. Jika tidak, tanda akan menjadi tidak betul, yang bermaksud bahawa angka secara keseluruhan akan menjadi tidak sekata atau tidak sama sekali. Sangat disyorkan untuk menggunakan pembaris.
2. Mula memotong templat. Gunting mesti melepasi dengan ketat sepanjang garis putus-putus. Jika tidak, tidak mungkin untuk melekatkan semua elemen angka itu bersama-sama. Walau bagaimanapun, anda tidak boleh tergesa-gesa, kerana templat boleh rosak dengan mudah oleh pergerakan cuai. Adalah penting bahawa semua elemen segi tiga templat mempunyai sisi yang sama. Ini adalah salah satu sifat utama icosahedron. Ia adalah sama penting dan wajib seperti syarat bahawa semua sisi petak yang sama sentiasa sama. Sekiranya peraturan ini dilanggar, perbezaan antara pihak akan sangat ketara.
3. Selepas memotong kosong, mula membengkokkan angka itu. Pembaris pasti diperlukan di sini. Titik lipatan akan ditunjukkan sebagai garisan pepejal, dan pelekatan harus dilakukan di sepanjang garis putus-putus. Matlamat utama adalah untuk menyambung dengan betul semua muka unsur segi tiga angka itu. Jika atas sebab tertentu anda tidak mempunyai gam PVA di tangan, dan sebaliknya anda menemui pelekat yang cepat kering, maka anda harus ingat bahawa tidak ada ruang untuk kesilapan. Jika anda menyambungkan bahagian dengan salah dan gam kering dalam masa beberapa saat, unsur-unsur tidak dapat dipisahkan lagi. Jika anda bekerja dengan gam PVA, anda perlu menekan dengan kuat pada setiap sambungan. Selepas menggunakan gam, pastikan bahagian itu ditekan antara satu sama lain selama kira-kira 20 saat.
4. Hiaskan produk siap. Untuk ini, anda boleh menggunakan cat, penanda, pensel, pastel. Anda juga boleh melampirkan benang pada angka siap untuk dapat menggantungnya. Selalunya kraf kertas seperti itu digunakan sebagai hiasan pokok Krismas untuk Tahun Baru.

Penggunaan icosahedron boleh berbeza. Ia boleh melakukan bukan sahaja estetik tetapi juga fungsi praktikal.

Icosahedron pelbagai warna

Icosahedron (corak untuk pelekatan boleh diwarnakan) pelbagai warna boleh menjadi bantuan visual yang baik apabila mempelajari warna warna dengan anak bongsu.

Untuk menghasilkan icosahedron berbilang warna, anda memerlukan bahan dan alat berikut:

• templat siap pakai (boleh didapati dengan mudah di Internet);
• kertas berwarna (jika anda tidak mempunyai apa-apa, anda boleh mewarna kertas putih dengan pen, cat atau pensel, yang akan menjadi menarik dan menghiburkan untuk kanak-kanak);
• gam (disyorkan untuk menggunakan PVA pengeringan lama);
• gunting.

Setelah semuanya disediakan, anda boleh meneruskan terus ke proses penciptaan, yang terdiri daripada peringkat berikut:

1. Buat kosong menggunakan stensil. Bagi bilangan warna yang berbeza, ia boleh mengikut budi bicara orang yang membuat kraf itu. Walau bagaimanapun, semakin banyak warna terang yang berbeza, semakin kanak-kanak akan menyukai produk ini. Anda boleh mengambil, sebagai contoh, warna utama pelangi. Anda boleh menambah beberapa warna lagi atau, sebaliknya, keluarkan warna yang kelihatan tidak perlu (contohnya, tidak perlu untuk satu angka mempunyai kedua-dua biru dan biru muda).
2. Sambungkan semua elemen menggunakan gam PVA yang kering lama.

Ikosahedron berbintang

Icosahedron berbintang adalah salah satu yang paling sukar dibuat. Walau bagaimanapun, keseluruhan kesukaran terletak pada hakikat bahawa anda perlu mempunyai banyak kesabaran. Kerja akan mengambil banyak masa.

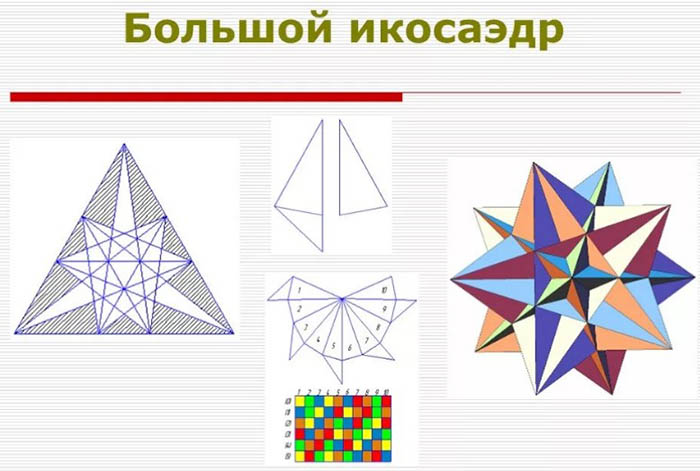
Selain kesabaran, anda perlu:

• gunting;
• kertas berwarna;
• gam.

Anda boleh menyediakan beberapa elemen hiasan untuk menghiasi produk siap. Ini boleh menjadi apa-apa objek yang kelihatan cantik: benang berwarna, reben, manik pelekat.

Setelah semua yang diperlukan disediakan, anda boleh meneruskan terus ke proses kreatif, yang terdiri daripada peringkat berikut:

1. Potong 30 petak dari kertas dengan sisi 5 cm setiap satu. Setiap petak sedemikian mesti mempunyai keluasan 25 persegi. lihat. Dalam kes ini, anda harus menggunakan kertas 3 warna. Ini boleh menjadi sebarang nada, contohnya, hijau, biru dan merah. Pada akhirnya perlu ada 10 petak setiap warna.
2. Apabila bilangan petak yang diperlukan telah dipotong, anda boleh mengambil salah satu daripadanya dan lipat dua. Kemudian setiap separuh perlu dibengkokkan ke arah tengah, diluruskan dan sudut bertentangan dilipat dua kali.
3. Jadikan helaian kertas kelihatan seperti tanda klasik, yang selalunya dibuat daripada kertas. Untuk melakukan ini, lipat sudut besar dari bahagian bawah.
4. Pegang bahagian lain petak itu. Ia perlu diterbalikkan, kemudian bahagian atas hendaklah dilipat untuk membentuk sampul surat. Dalam kes ini, sudut akutnya mesti dimasukkan ke dalam produk.

5. Teruskan bekerja dengan petak pertama. Sekarang bahawa ia telah bertukar menjadi sampul surat, anda perlu melipatnya separuh dan lipat telinga yang menonjol, mengarahkannya ke sudut luar segitiga. Seterusnya, selepas meluruskan, unit pemasangan dibentuk.
6. Untuk melakukan bahagian kerja yang paling lama, kesemua 5 langkah yang diterangkan di atas hendaklah diulang dengan setiap 29 petak yang tinggal. Ini akan memerlukan banyak kesabaran. Anda mungkin tidak boleh membuat kesemua 30 model yang diperlukan serentak. Adalah disyorkan untuk berehat daripada proses kreatif ini.
7. Apabila kesemua 30 bahagian sudah sedia, anda boleh mengambil salah satu daripadanya dan tolak hujungnya ke dalam poket bahagian lain (semestinya berwarna berbeza). Oleh itu, sudut elemen ini harus dimuatkan ke dalam poket bahagian ketiga, yang berbeza dalam warna daripada dua yang lain. Sudut bahagian ke-3 hendaklah dimuatkan ke dalam poket bahagian ke-4, yang akan menjadi warna yang sama dengan bahagian pertama. Dengan cara ini warna akan silih berganti.
8. Masukkan hujung bahagian ke-3 ke bahagian ke-2. Bahagian pertama dimasukkan ke dalamnya, dan hujung bahagian kedua dikeluarkan ke dalam poket pautan pertama.
9. Masukkan teka-teki ke-2 ke dalam teka-teki ke-3, kemudian teka-teki pertama ke dalamnya, dan semuanya ditutup dengan teka-teki ke-3.
10. Pasang semua elemen mengikut rajah di atas. Sebaik sahaja elemen terakhir telah disediakan, kerja yang panjang dan teliti untuk membuat icosahedron berbintang boleh dianggap lengkap.

Icosahedron hiasan

Badan geometri 20 segi yang diperbuat daripada kertas menggunakan teknik kusudama ini akan kelihatan hebat pada pokok perayaan pada Malam Tahun Baru. Untuk membuat icosahedron hiasan, anda perlu memotong 30 petak dari kertas. Lebih baik jika ia berwarna kuning muda.

Setelah menyediakan bilangan petak kertas yang diperlukan, anda boleh memulakan proses kreatif:

1. Ambil salah satu petak (semuanya sama, jadi anda boleh mengambil mana-mana satu), lipat dua, dan bengkokkan sisi ke tengah.
   Kemudian bahan kerja dibentangkan dan kemudian dilipat di sepanjang garis tengah. Tepi perlu dilipat ke arah tengah dan kemudian dibuka semula.
2. Bengkokkan kepingan supaya segi empat sama bertukar menjadi segi tiga. Selepas ini, ia mesti diluruskan dan bahagian sisi bengkok ke arah garis tengah. Kemudian salah satu tepi bawah hendaklah dilipat ke tepi. Hasilnya harus menjadi sudut. Sisi bertentangan perlu dilipat ke arah tengah untuk membentuk hidung mancung.
3. Ulangi keseluruhan prosedur di atas sekali lagi, tetapi sekarang dengan bahagian ke-2 bahagian. Hasilnya ialah segi empat sama dengan sepasang muncung berbentuk segi tiga.
4. Teka-teki itu perlu dilipat memanjang, dengan salah satu daripada dua segitiga dilipat ke hadapan dan satu lagi ke arah yang bertentangan.
   Seterusnya, bahagian itu perlu diluruskan. Untuk melakukan ini, anda perlu menarik hujungnya. Ini akan mencipta pautan pertama ikosahedron hiasan. Walau bagaimanapun, perlu ada 30 pautan sedemikian secara keseluruhan, jadi prosedur dilakukan 29 kali lagi.
5. Apabila semua 30 elemen sudah sedia, anda boleh mula menyambungkannya. Ini dilakukan seperti berikut: hujung satu pautan mesti dimasukkan ke dalam poket yang lain; kemudian hujung pautan ke-3 dimasukkan ke dalam poket yang sama; dan hujung ke-4 diulirkan melalui ke-5; kemudian yang pertama dimasukkan ke dalam yang ke-5, menghasilkan cincin tertutup.
6. Semua hujung kelopak seterusnya perlu diletakkan di ruang antara pautan untuk membentuk segi tiga.
7. Setiap bahagian mesti tertakluk kepada prosedur yang sama. Selepas menutup segitiga terakhir, satu angka cantik terbentuk yang akan kelihatan hebat di pokok percutian.

Setelah memahami cara membuat corak kertas untuk melekatkan icosahedron, anda boleh mula memodelkannya sendiri, menggunakan pelbagai penyelesaian warna, bahan dan hiasan.

Video tentang membuat icosahedron daripada kertas

Kelas induk untuk membuat icosahedron dengan lubang: